光学镜片表面质量核心指标解析:PV值与RMS值的特性及应用
镜片表面的面型精度是决定光学系统性能的关键因素——从消费电子领域的手机摄像头镜片,到航空航天领域的卫星遥感光学组件,即便微米级甚至纳米级的表面误差,都可能导致成像失真、能量损耗等严重问题。此前,“深度追光”平台的“追光者”已就光学镜片研磨抛光质量展开探讨,而实践中,光学加工、设计及检测人员常对PV值(峰谷值)与RMS值(均方根值)的定义、差异及适用场景存在困惑。本文将系统拆解这两大核心指标,结合专业原理与实际应用,为光学从业者提供清晰的参数解读框架。

一、PV值(PeaktoValleyValue):聚焦表面误差的极端偏差
PV值即峰谷值,其核心功能是量化光学表面指定区域内的最大面型偏差,直观反映表面误差的“极限状态”,是评估镜片加工精度的重要参考。
1.定义与物理意义
从物理本质来看,PV值指光学表面去除理想基准面后,测量区域内最高点(波峰)与最低点(波谷)之间的垂直距离,可通过2D轮廓线或3D面型数据进行表征。若将光学表面类比为微观地形,PV值即对应地形中最高山峰顶端与最深山谷谷底的垂直落差。
例如,当某镜片的PV值为500纳米时,意味着其表面凸起的最高处与凹陷的最低处相差500纳米——尽管该数值远小于头发丝直径(约50100微米),但对于高精度光学系统(如激光雷达、显微成像设备)而言,此类偏差可能直接引发像差,导致成像出现“鬼影”、光斑扩散或边缘模糊,严重影响系统功能。
2.主要计算类型及特性
由于测量环境、数据处理方式的差异,PV值存在多种计算形式,其准确性与参考价值差异显著,需在实际应用中加以区分:
直接PV(SimplePV):计算逻辑最为直接,即通过公式“PV=Y_maxY_min”(Y_max为测量区域内最高点坐标,Y_min为最低点坐标)获取结果。但该方法对局部异常点(如表面附着的尘埃、细微划痕、测量噪声)极为敏感,易因偶然因素导致PV值虚高,无法真实反映镜片的整体面型精度,目前已较少单独用于专业检测。
RMSPV(PVr):为规避直接PV的局限性,需先对原始测量数据进行预处理(如剔除倾斜、像散等系统性干扰),再计算处理后数据的峰谷差。相较于直接PV,RMSPV的抗干扰能力更强,结果更具代表性,但仍未完全脱离局部异常点的潜在影响。
PVviaZernike(PVq):当前光学行业公认的最优计算方式。该方法通过泽尼克多项式对测量数据进行拟合——泽尼克多项式可精准描述光学系统中常见的离焦、像散、彗差等像差,拟合过程相当于过滤掉表面划痕、尘埃等非面型误差因素,仅保留镜片本身的面型偏差。因此,PVq能最真实地反映镜片加工质量,是光学检测与验收的主流标准。
二、RMS值(RootMeanSquareValue):表征整体波动的统计指标
RMS值即均方根值,基于统计原理量化光学表面所有测量点相对于理想基准面的偏差程度,聚焦表面误差的“整体分布特征”,是预测光学系统整体性能的关键参数。
1.定义与物理意义
RMS值的核心是通过统计方法计算表面误差的平均波动水平:若仍以微观地形类比,其并非关注“最高山与最深谷的落差”,而是量化整个区域内所有点位海拔相对于理想平面的平均起伏程度。例如,某镜片表面无显著高凸或深凹区域,但存在连续平缓的微起伏,其PV值可能较小,而RMS值会因整体波动频繁而偏高。
从光学性能来看,RMS值直接影响系统的散射损耗与斯特列尔比(StrehlRatio,衡量成像质量的核心指标):RMS值越低,表面越接近理想平面,光线被散射至非目标方向的概率越小,成像的能量集中度与对比度越高。以激光遥感系统为例,若镜片RMS值超标,会导致激光能量分散,直接缩短探测距离并降低信号信噪比。
在实际检测中,干涉仪等专业设备会自动完成上述计算,从业者无需手动运算,只需通过结果判断表面整体波动是否符合设计要求即可。
三、PV值与RMS值的核心差异及协同应用
PV值与RMS值并非“优劣对立”的关系,二者分别从“极端偏差”与“整体波动”两个维度描述表面质量,需结合应用场景协同分析,具体差异可通过下表清晰呈现:
| 对比维度 | PV 值(峰谷值) | RMS 值(均方根值) |
|---|---|---|
| 敏感性 | 对局部缺陷(尘埃、划痕)敏感性高,易受偶然因素影响 | 基于全点统计,受局部异常点影响小,结果稳定性强 |
| 光学影响 | 主要引发像差(球差、彗差等),影响成像质量 | 主要导致散射损耗,影响能量效率与斯特列尔比 |
| 应用侧重 | 光学加工环节:反映加工难度,指导抛光工艺优化 | 光学设计环节:预测系统整体性能,明确指标要求 |
| 数值关联性 | 对于平滑光学表面,PV 值通常为 RMS 值的 3-5 倍(PV≈3-5RMS),具体比例取决于误差分布类型 | - |
典型案例:相同PV值下的RMS值差异
某实验中,三个镜片表面的PV值均为1(即波峰与波谷落差一致),但面型形态存在显著差异:
镜片1:单一高凸区域与单一深凹区域并存,其余区域接近理想平面;
镜片2:无明显高凸或深凹,整体呈连续平缓的微起伏;
镜片3:中等幅度的起伏分布,无极端偏差点。
经计算,三者的RMS值分别为0.5、0.15、0.31——该案例表明,PV值仅能反映表面的“最差情况”,无法区分整体面型的波动特征;而RMS值可通过全点统计,精准体现表面的整体质量差异,二者结合才能全面评估镜片性能。
四、光学检测报告解读要点
在解读光学镜片检测报告时,需重点关注以下两点,避免因参数理解偏差导致误判:
1.明确PV值的计算类型:报告中若仅标注“PV值”,需进一步确认其具体计算方式——优先选择PVviaZernike(PVq)结果,因其已过滤局部干扰,更能反映真实加工质量;若为直接PV或RMSPV,需结合实际应用场景评估其参考价值,必要时补充PVq检测。
2.避免单一指标依赖:高性能光学系统需PV值与RMS值“双达标”。例如,航天级光学镜片通常要求PV值≤λ/4(λ为工作波长,约500纳米)、RMS值≤λ/20,既确保无极端偏差引发严重像差,又保证整体表面平整性以降低散射损耗,从而兼顾成像质量与能量效率。
PV值与RMS值作为光学镜片表面质量的核心指标,分别从“极端偏差”与“整体波动”维度为从业者提供关键参考。光学加工人员可通过PV值(尤其是PVq)优化抛光工艺,攻克面型精度难点;设计人员可依托RMS值精准预测系统性能,制定合理的指标规范。后续将进一步探讨“PVviaZernike(PVq)的优势原理”及“TWE、RWE等测试方法的差异”,助力从业者深化光学参数认知,推动光学系统性能提升。
-

半导体抛光设备自动化应用及工艺质量管控要点探析
在半导体器件规模化量产进程中,抛光工艺作为保障晶圆加工精度与表面质量的核心环节,其设备自动化水平、工艺参数调控能力、检测体系完善度及异常处置效率,直接决定生产效率、工艺稳定性与产品良率。本文从抛光设备自动化配置要求、核心工艺参数调控、关键检测指标界定及常见工艺异常处理四个维度,系统阐述半导体抛光工艺的质量管控核心要点,为半导体抛光制程的标准化、精细化实施提供参考。
2026-02-12
-
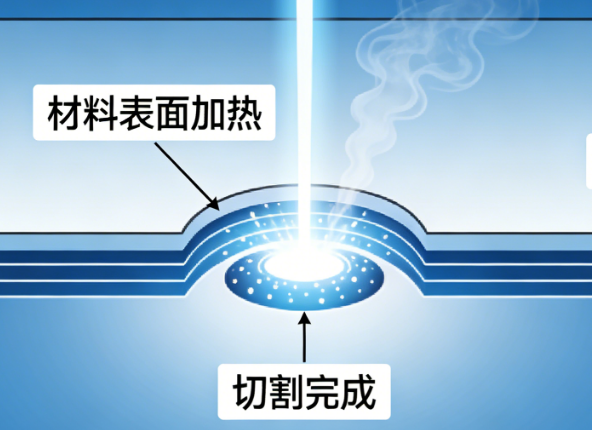
硅晶圆激光切割核心技术深度解析:原理、工艺与质量把控
在半导体制造产业链中,硅晶圆切割是芯片成型的关键工序,其加工精度与效率直接影响芯片良品率和产业发展节奏。随着微电子器件向微型化、薄型化升级,传统切割方式的弊端逐渐显现,激光切割凭借高精度、低损伤的技术优势成为行业主流。本文从激光切割系统的硬件构成出发,深入拆解隐形切割与消融切割两大核心工艺,解析光斑、焦点的精度控制逻辑,并探讨切割质量的评价维度与效率平衡策略,系统梳理硅晶圆激光切割的核心技术体系
2026-02-12
-
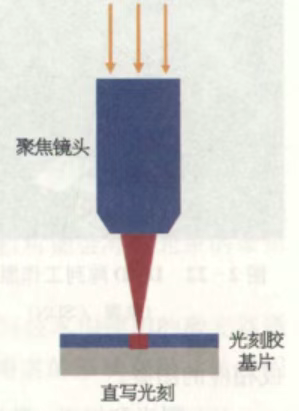
无掩模激光直写技术研究概述
无掩模激光直写技术作为微纳加工领域的先进光刻技术,摒弃了传统光刻工艺对掩模版的依赖,凭借直接写入的核心特性,在复杂微纳结构制备、高精度图案加工中展现出独特优势,成为微纳加工领域的重要技术方向。本文从工作原理与流程、技术特性、现存挑战、分辨率与对准参数、核心设备及厂务动力配套要求等方面,对该技术进行全面梳理与阐述。
2026-02-12
-

SiC功率器件的高温时代:封装成为行业发展核心瓶颈
在半导体功率器件技术迭代进程中,碳化硅(SiC)凭借高温工作、高电流密度、高频开关的核心优势,成为推动功率半导体升级的关键方向,其普及大幅提升了器件的功率密度与工作效率,为功率半导体行业发展带来全新机遇。但与此同时,行业发展的核心瓶颈正悄然从芯片设计与制造环节,转移至封装层面。当SiC将功率器件的工作温度与功率密度不断推高,芯片本身已具备承受更高应力的能力,而封装环节的材料适配、热路径设计等问题却日益凸显,高温与快速功率循环叠加的工况下,焊料与热路径成为决定SiC功率模块寿命的核心因素,封装技术的发展水平,正成为制约SiC功率器件产业化落地与长期可靠应用的关键。
2026-02-12







