透镜磨边工艺技术研究:中心误差校正机制与关键工序解析
在光学仪器(如成像镜头、显微光学系统、视光镜片等)的制造流程中,透镜作为核心光学元件,其光学性能直接决定了整机的成像质量与使用精度。透镜加工过程中,受铣磨定位偏差、精磨精度波动、抛光工艺误差等因素影响,易产生“中心误差”,导致透镜光轴与基准轴偏离,严重制约光学系统性能。磨边工艺作为校正中心误差、保障透镜精度的核心技术环节,其原理与工艺控制对光学产品品质具有决定性作用。本文从中心误差的定义与表征入手,系统拆解磨边工艺的核心步骤、定心方法及倒角工序,为深入剖析该关键光学加工技术提供参考。
1透镜中心误差的定义及表征参量
1.1中心误差的本质定义
透镜中心误差,是指透镜在铣磨、精磨、抛光等加工环节中,因各类误差叠加导致光轴(透镜实现光学作用的核心轴线)与基准轴(用于标注、检验及校正中心误差的基准线,需结合透镜安装表面形态与装夹条件,且需与系统光轴保持一致)无法重合而产生的偏差。
该误差的核心度量指标为“面倾角θ”,单位为分(′)或秒(″),其定义为:透镜光学表面定心顶点处的法线与基准轴之间的夹角。其中,“定心顶点”特指光学表面与基准轴的交点,是中心误差测量的关键基准点位。
1.2中心误差的辅助表征参量
工业生产中,为更直观、精准地描述中心误差,除面倾角外,还需通过以下三类参量进行辅助表征:
中心偏(偏心差c):单位为毫米(mm),指透镜几何轴(即透镜外圆的中心轴线)与光轴在透镜中心位置的偏离距离,直接反映几何轴与光轴的对齐程度。
球心偏a:单位为毫米(mm),指透镜光学表面的曲率中心相对于基准轴的偏移量,是评估光学曲面定位精度的核心指标。
边厚差Δt:单位为毫米(mm),指透镜边缘不同点位的厚度差值,是判断中心误差的直观依据——中心误差越大,边厚差数值越显著。
2磨边工艺的核心流程:定心与磨削两步法
磨边工艺的核心目标是“校正中心误差,实现透镜光轴与基准轴的精准重合”,需在专用定心磨边机上完成(机床回转轴即为磨边后透镜的基准轴,最终转化为透镜几何轴),整个流程分为“定心”与“磨削”两个不可逆的关键步骤。
2.1第一步:定心——确定光轴与基准轴的重合位置
定心是磨边工艺的前置核心环节,需通过特定技术手段定位透镜的“理想安装位置”:即使透镜光学表面定心顶点处的法线与基准轴(即机床回转轴)完全重合。此步骤完成后,透镜光轴与基准轴已实现精准对齐,为后续外圆磨削奠定精度基础。
2.2第二步:磨削——加工外圆至设计尺寸
在定心工序完成的基础上,机床以基准轴为中心,对透镜外圆进行磨削加工。加工过程中需严格控制磨削精度,将外圆直径加工至设计要求数值,同时确保外圆几何轴与已对齐的光轴保持完全重合。至此,透镜中心误差得到有效校正,可满足后续装配与光学系统使用需求。
3核心定心方法:机械定心的原理与参数控制
工业领域常用的定心方法包括光学定心法、机械定心法、光电定心法及激光定心法。其中,机械定心法因操作简便、适配性广、成本可控等优势,成为多数光学制造企业的首选工艺(原文提及“光学定心法目前暂未应用”,故本文重点解析机械定心技术)。
3.1机械定心的装置结构与工作原理
机械定心装置主要由“一对高精度同轴定心夹头”“待定心透镜”及“压力调节弹簧”组成(装置示意图中:1、3为定心夹头,2为待定心透镜,4为弹簧),其工作机制以“受力平衡”为核心,具体流程如下:
1.初始状态:透镜刚完成装夹时,其光轴与夹头轴线(即基准轴)未对齐,夹头端面仅与透镜表面形成单点接触。
2.受力分解:接触点产生的作用力P可分解为“垂直于夹头端面的分力F1”与“垂直于夹头轴线的分力F2”。其中,F1与另一夹头的反作用力形成平衡,F2则推动透镜沿垂直于轴线的方向移动。
3.平衡状态:当透镜移动至“夹头端面与透镜表面的接触点轨迹形成完整圆形”时,透镜进入受力平衡状态,其两面的曲率中心均精准落在夹头轴线上——此时,透镜光轴与基准轴实现完全重合,定心工序完成。
3.2机械定心的关键参数:定心角与Z系数
机械定心的成功率与精度,取决于“定心角α”与“Z系数”两大核心参数,二者直接决定定心工艺的可行性与稳定性。
3.2.1定心角α的定义与工艺影响
定心角α,是指在夹头轴线平面内,透镜与夹头接触点的切线之间的夹角,其数值大小与定心难度呈正相关,具体划分标准如下:
当α≥17°30′时,定心工艺易实现,无需额外调整工艺参数;
当8°≤α≤17°30′时,定心工艺难度中等,需优化夹头压力、装夹力度等参数;
当α≤8°时,定心工艺难以实现,需更换夹头规格或调整透镜加工方案。
3.2.2Z系数的计算与应用
Z系数是连接“夹头直径、透镜曲率半径”与“定心角”的关键桥梁,需通过公式计算得出,其结果直接用于判断定心工艺的可行性。
(1)Z系数计算公式
Z=|(D1/R1±D2/R2)/4|
公式中参数定义如下:
D1、D2:定心夹头的直径(根据透镜设计尺寸选择适配规格);
R1、R2:透镜两面的曲率半径;
符号规则:双凸透镜、双凹透镜取“+”号;一凸一凹透镜取“”号;若透镜某一面为平面(曲率半径趋近于无穷大),则对应项取值为0。
(2)Z系数与定心工艺的对应关系
由公式α=2arcsinZ可推导,Z系数与定心角、定心难度存在明确对应关系,具体如下表所示:
| Z 系数范围 | 对应定心角 | 定心工艺难度 |
|---|---|---|
| Z≥0.15 | α≥17°30′ | 较易实现 |
| 0.07<Z<0.15 | 8°<α<17°30′ | 较困难 |
| Z≤0.07 | α≤8° | 难实现 |
在实际生产中,可先根据透镜曲率半径与选定的夹头直径计算Z系数,再依据上述对应关系判断定心工艺的可行性。若Z≤0.07,需及时调整夹头直径规格或优化透镜加工方案,以保障定心精度。
4倒角工序:透镜加工的功能性保障环节
磨边工艺完成后,需对透镜边缘进行倒角处理。该工序并非仅为外观优化,而是兼具“结构保护”与“工艺辅助”的功能性环节,具体可分为两类:
4.1结构性倒角
结构性倒角的核心作用是保障透镜后续装配与光学性能:一方面,可避免透镜在装入镜框时因边缘尖锐导致的破损、崩边;另一方面,可通过精准控制倒角尺寸,限定透镜的有效孔径,确保光线仅通过光学有效区域,避免边缘杂光干扰,保障成像质量。
4.2工艺性倒角
工艺性倒角主要用于保护加工过程中的透镜工件:未倒角的透镜边缘尖锐,在搬运、清洗及后续工序(如镀膜、检测)中易产生崩裂、划痕,导致工件报废。通过工艺性倒角,可在透镜边缘形成圆润过渡面,降低加工过程中的损伤风险,提升成品率。
5结语
透镜磨边工艺作为光学制造中的关键环节,看似单一,实则是“误差控制、参数优化、工序协同”的精密技术体系。从中心误差的多维度表征,到定心工序的受力平衡原理,再到Z系数与定心角的精准计算,每一步均需严格把控,方能保障透镜光轴与基准轴的精准对齐;而倒角工序的补充,进一步实现了“精度”与“可靠性”的双重保障。
在光学制造技术持续升级的背景下,深入理解磨边工艺的核心原理,不仅可为从业者优化工艺参数、提升产品品质提供理论支撑,更能为探索更高效的定心技术(如激光定心、光电定心)奠定基础。毕竟,光轴的精准对齐,始终是保障光学产品性能的核心前提。
-

半导体抛光设备自动化应用及工艺质量管控要点探析
在半导体器件规模化量产进程中,抛光工艺作为保障晶圆加工精度与表面质量的核心环节,其设备自动化水平、工艺参数调控能力、检测体系完善度及异常处置效率,直接决定生产效率、工艺稳定性与产品良率。本文从抛光设备自动化配置要求、核心工艺参数调控、关键检测指标界定及常见工艺异常处理四个维度,系统阐述半导体抛光工艺的质量管控核心要点,为半导体抛光制程的标准化、精细化实施提供参考。
2026-02-12
-
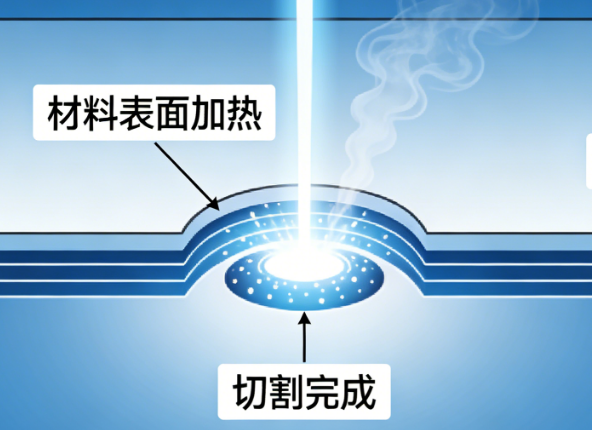
硅晶圆激光切割核心技术深度解析:原理、工艺与质量把控
在半导体制造产业链中,硅晶圆切割是芯片成型的关键工序,其加工精度与效率直接影响芯片良品率和产业发展节奏。随着微电子器件向微型化、薄型化升级,传统切割方式的弊端逐渐显现,激光切割凭借高精度、低损伤的技术优势成为行业主流。本文从激光切割系统的硬件构成出发,深入拆解隐形切割与消融切割两大核心工艺,解析光斑、焦点的精度控制逻辑,并探讨切割质量的评价维度与效率平衡策略,系统梳理硅晶圆激光切割的核心技术体系
2026-02-12
-
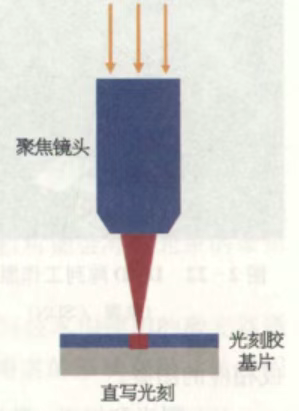
无掩模激光直写技术研究概述
无掩模激光直写技术作为微纳加工领域的先进光刻技术,摒弃了传统光刻工艺对掩模版的依赖,凭借直接写入的核心特性,在复杂微纳结构制备、高精度图案加工中展现出独特优势,成为微纳加工领域的重要技术方向。本文从工作原理与流程、技术特性、现存挑战、分辨率与对准参数、核心设备及厂务动力配套要求等方面,对该技术进行全面梳理与阐述。
2026-02-12
-

SiC功率器件的高温时代:封装成为行业发展核心瓶颈
在半导体功率器件技术迭代进程中,碳化硅(SiC)凭借高温工作、高电流密度、高频开关的核心优势,成为推动功率半导体升级的关键方向,其普及大幅提升了器件的功率密度与工作效率,为功率半导体行业发展带来全新机遇。但与此同时,行业发展的核心瓶颈正悄然从芯片设计与制造环节,转移至封装层面。当SiC将功率器件的工作温度与功率密度不断推高,芯片本身已具备承受更高应力的能力,而封装环节的材料适配、热路径设计等问题却日益凸显,高温与快速功率循环叠加的工况下,焊料与热路径成为决定SiC功率模块寿命的核心因素,封装技术的发展水平,正成为制约SiC功率器件产业化落地与长期可靠应用的关键。
2026-02-12







