什么是傅里叶变换?从理论突破到跨领域应用全面了解傅里叶变换
当人类聆听交响乐时,听觉系统可清晰分辨长笛的清亮、小提琴的婉转与低音提琴的厚重——这一过程背后,隐含着一种重塑现代科技格局的数学方法:傅里叶变换。它通过拆解复杂信号、重组基础频率的核心逻辑,不仅推动了数学领域的革新,更成为连接理论与现实应用的关键桥梁,广泛渗透于音频处理、图像压缩、科学研究等诸多领域。

一、理论溯源:傅里叶与热传导研究的突破
傅里叶变换的提出,源于19世纪法国数学家让巴蒂斯特·约瑟夫·傅里叶对热传导现象的探索,其个人经历与时代背景共同促成了这一理论的诞生。
傅里叶生于1768年法国革命前夕,10岁时沦为孤儿,后在故乡欧塞尔的修道院接受教育。青年时期,他曾在宗教奉献与数学研究之间徘徊,最终放弃宗教训练,投身教育事业。法国大革命期间,傅里叶积极参与革命活动,却在1794年恐怖统治时期因被指控持有“反革命信仰”入狱,濒临处决。直至恐怖统治结束,他才得以重返学术领域,于1795年恢复数学教学工作。此后,傅里叶被任命为拿破仑·波拿巴的科学顾问,随军队入侵埃及时,在研究埃及古物的同时,开始聚焦热传导的数学规律——这一研究成为傅里叶变换的思想起点。
在对热传导的观察中,傅里叶发现:当金属杆一端被加热后,热量会逐步扩散至整体,最终实现温度均衡。基于这一现象,他提出了颠覆性观点:热量的分布可通过一组基础波(即频率)的叠加表示。金属冷却过程中,高能高频波率先衰减,低频波随后沉寂,类似交响乐收尾时各声部依次静默的规律。
这一观点在当时引发了数学界的质疑。1807年,傅里叶在巴黎研究所汇报研究时,著名数学家约瑟夫路易斯·拉格朗日直言该理论“几乎不具备可行性”。同行的核心质疑集中于“不规则热量分布”——例如金属杆一半冷、一半热的状态,温度存在明显突变,而当时主流观点认为,平滑的波函数无论如何叠加,都无法形成“尖角状”的突变。傅里叶则坚持:只要叠加无限组简单曲线,即可描述此类不规则状态。随着数学理论的发展,后世证实了傅里叶的核心逻辑正确性,普林斯顿大学数学家查尔斯·费弗曼曾形象阐释:“若将不同频率的音叉精准调校,其共同振动可还原贝多芬《第九交响曲》的完整旋律”,这恰是傅里叶理论的直观体现。
二、核心原理:函数的“拆解”与“重组”
从数学本质而言,傅里叶变换是一种将复杂函数分解为基础频率组件,并通过组件重组还原原始函数的运算方法,其核心逻辑可概括为“扫描判定叠加”三个步骤。
1.运算逻辑:频率贡献度的判定
傅里叶变换以“频率”为分析单位,通过将原始函数与不同频率的正弦波、余弦波相乘,判定各频率对原始函数的贡献度。具体而言:
若原始函数与某一频率(如频率3)的波函数相乘后,结果呈现大量高幅值“峰值”,且峰值平均高度显著,则说明该频率对原始函数的贡献度高,是核心组成部分;
若相乘结果中“峰值”与“谷值”相互抵消,平均值趋近于零(如频率5),则说明该频率对原始函数无实质贡献,可排除于核心组件之外。
在数学框架下,傅里叶变换以复平面为运算载体,融合实数与虚数实现对所有潜在频率的扫描,最终将复杂函数简化为一组“频率贡献度”数据,使原本难以求解的数学问题在“频率维度”下变得简洁可解。
2.特殊场景:傅里叶级数的应用
对于具有“锋利边缘”的函数(如数字信号中常见的方波),傅里叶变换需通过无限组频率叠加逼近边缘,这一无限频率集合被称为“傅里叶级数”。尽管早期数学界对“无限级数”的合理性存在争议,但随着调和分析分支的发展,傅里叶级数已成为函数分析的核心工具之一,为数字信号处理、电路设计等领域提供了理论支撑。
3.高维拓展:从一维到二维的应用延伸
傅里叶变换不仅适用于一维函数(如声波),还可拓展至二维乃至更高维度的对象(如图像)。以灰度图像为例,其可被视为一个“二维函数”——像素坐标对应函数的自变量,像素亮度对应函数的因变量。傅里叶变换会将该函数分解为一组二维频率组件,这些组件表现为不同方向的“条纹图案”,类似棋盘格的基础单元。通过这些基础图案的组合,可还原任意灰度图像,为图像处理技术奠定了理论基础。
三、跨领域应用:从日常科技到前沿研究
傅里叶变换的广泛应用,离不开1960年代的关键技术突破——数学家詹姆斯·库利(JamesCooley)与约翰·图基(JohnTukey)提出“快速傅里叶变换(FFT)”算法,大幅降低了运算复杂度,使傅里叶变换从“理论工具”转向“实际应用”。如今,其应用已覆盖日常科技与前沿科学,成为现代技术体系的重要支撑。
1.日常科技领域:数据压缩与信号优化
图像压缩:JPEG格式是傅里叶变换的典型应用。以8×8像素的图像块为例,傅里叶变换可将其分解为64种基础条纹图案,压缩算法通过删除对应“细节信息”的高频组件(人眼对高频细节敏感度低),在大幅缩小文件体积的同时,保持图像视觉效果基本不变,这一技术成为数字图像存储与传输的核心标准;
音频处理:在音频录制与优化中,傅里叶变换可精准识别背景噪音(多为高频信号),通过过滤无用高频组件实现降噪;同时,其可分离音频中的不同声部与乐器频率,为音乐制作、语音识别提供技术支持。
2.前沿科学领域:从宏观到微观的探索
天文学与物理学:天文学家用傅里叶变换分析潮汐的周期性变化,推导引力波的信号特征;在量子力学中,傅里叶变换为“不确定性原理”提供了数学基础——描述粒子位置的函数与其傅里叶变换(对应粒子动量)存在互补关系:若位置函数呈现“尖峰”(位置确定度高),则动量函数会高度分散(动量确定度低),反之亦然;
医学领域:磁共振成像(MRI)技术通过傅里叶变换处理人体组织的电磁信号,将复杂信号分解为基础频率组件,再通过组件重组生成人体内部结构图像,为疾病诊断提供精准依据。
四、学术意义:数学理论的现实价值
傅里叶变换的发展历程,印证了抽象数学对现实世界的深刻影响。从傅里叶最初对热传导的好奇,到衍生出“调和分析”这一数学分支,再到推动跨领域技术革新,其核心价值在于为“复杂系统的解读”提供了统一范式——无论是声波、图像,还是引力波、量子信号,都可通过“频率分析”的逻辑拆解为可理解、可处理的基础组件。
正如纽约大学与弗拉特iron研究所的莱斯利·格林加德所言:“傅里叶分析对数学的影响难以估量,它几乎触及数学、物理、化学等所有领域”。如今,傅里叶变换已融入日常生活的细微之处,从手机里的图像存储到医院的MRI检查,从音频降噪到引力波探测,其作为“数学基石”的作用,仍在持续推动科技与科学的进步。
-

半导体抛光设备自动化应用及工艺质量管控要点探析
在半导体器件规模化量产进程中,抛光工艺作为保障晶圆加工精度与表面质量的核心环节,其设备自动化水平、工艺参数调控能力、检测体系完善度及异常处置效率,直接决定生产效率、工艺稳定性与产品良率。本文从抛光设备自动化配置要求、核心工艺参数调控、关键检测指标界定及常见工艺异常处理四个维度,系统阐述半导体抛光工艺的质量管控核心要点,为半导体抛光制程的标准化、精细化实施提供参考。
2026-02-12
-
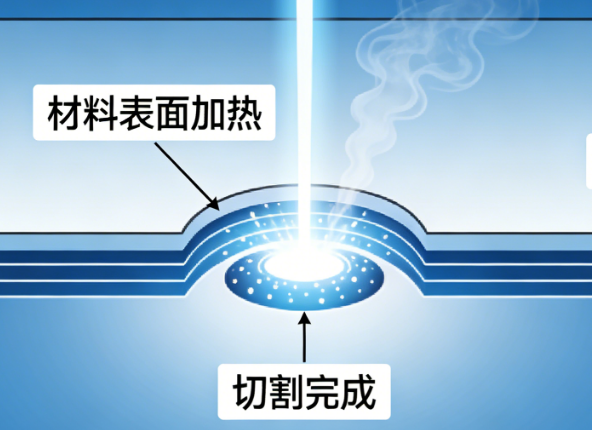
硅晶圆激光切割核心技术深度解析:原理、工艺与质量把控
在半导体制造产业链中,硅晶圆切割是芯片成型的关键工序,其加工精度与效率直接影响芯片良品率和产业发展节奏。随着微电子器件向微型化、薄型化升级,传统切割方式的弊端逐渐显现,激光切割凭借高精度、低损伤的技术优势成为行业主流。本文从激光切割系统的硬件构成出发,深入拆解隐形切割与消融切割两大核心工艺,解析光斑、焦点的精度控制逻辑,并探讨切割质量的评价维度与效率平衡策略,系统梳理硅晶圆激光切割的核心技术体系
2026-02-12
-
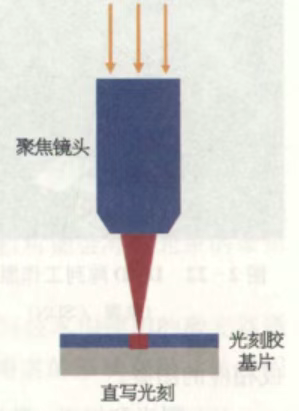
无掩模激光直写技术研究概述
无掩模激光直写技术作为微纳加工领域的先进光刻技术,摒弃了传统光刻工艺对掩模版的依赖,凭借直接写入的核心特性,在复杂微纳结构制备、高精度图案加工中展现出独特优势,成为微纳加工领域的重要技术方向。本文从工作原理与流程、技术特性、现存挑战、分辨率与对准参数、核心设备及厂务动力配套要求等方面,对该技术进行全面梳理与阐述。
2026-02-12
-

SiC功率器件的高温时代:封装成为行业发展核心瓶颈
在半导体功率器件技术迭代进程中,碳化硅(SiC)凭借高温工作、高电流密度、高频开关的核心优势,成为推动功率半导体升级的关键方向,其普及大幅提升了器件的功率密度与工作效率,为功率半导体行业发展带来全新机遇。但与此同时,行业发展的核心瓶颈正悄然从芯片设计与制造环节,转移至封装层面。当SiC将功率器件的工作温度与功率密度不断推高,芯片本身已具备承受更高应力的能力,而封装环节的材料适配、热路径设计等问题却日益凸显,高温与快速功率循环叠加的工况下,焊料与热路径成为决定SiC功率模块寿命的核心因素,封装技术的发展水平,正成为制约SiC功率器件产业化落地与长期可靠应用的关键。
2026-02-12







