光度学核心物理量的数学推导与应用探析
光度学作为建立在几何光学与辐射度量学基础上的严密学科,其核心价值在于精准描述光的传播规律及与物质的相互作用。光通量、发光强度、照度和亮度这四大物理量,构成了光度学的理论基石,其内在逻辑关系与数学推导不仅是学术研究的关键内容,更是光学设计、计算机图形学等工程领域的技术前提。本文将从立体角的微分定义出发,系统梳理四大物理量的数学本质、推导过程,并探讨其核心应用与实践价值。
一、数学基石:立体角的微分形式构建
在三维空间中,光的传播具有方向性特征,而立体角作为“方向”的量化指标,是所有光度学推导的基础。
(一)立体角的定义
二维平面中,角度定义为弧长与半径之比;延伸至三维空间,立体角Ω定义为球面表面积S与半径平方r²之比,其单位为球面度(sr)。这一定义为后续描述光在空间中的传播范围提供了量化依据。
(二)球坐标系下的微分推导
在球坐标系(r,θ,φ)中,θ为天顶角(0≤θ≤π),φ为方位角(0≤φ≤2π)。球面上的微元面积dA由经线方向弧长(rdθ)与纬线方向弧长(rsinθdφ)构成,因此微元面积表达式为:dA=r²sinθdθdφ。结合立体角定义Ω=S/r²,可推导出立体角的微分形式:dΩ=sinθdθdφ。这一公式是后续所有光度学积分运算的核心,通过对其在全球面范围内积分,可验证全球面立体角为4π球面度。
二、四大核心物理量的定义与数学推导
(一)光通量(Φ):光能量的总量表征
光通量是基于人眼视觉特性(视见函数V(λ))加权后的辐射通量,单位为流明(lm,1lm=683lm/W),是描述光总能量的基本标量,不涉及方向与位置信息。其物理意义在于量化光对人眼产生的视觉刺激总量,是光度学中最基础的物理量。
(二)发光强度(I):点光源的方向辐射密度
发光强度描述点光源在特定方向上的辐射密集程度,定义为单位立体角内的光通量,单位为坎德拉(cd,1cd=1lm/sr)。根据定义可建立其与光通量的数学关系:I=dΦ/dΩ,由此可推导出光通量的积分表达式Φ=∫IdΩ。对于各向同性点光源,发光强度I为常数,此时光通量Φ=4πI,该关系为点光源的光能量计算提供了简洁方法。
(三)照度(E):表面接收光的密度量化
照度定义为照射到物体单位表面积上的光通量,单位为勒克斯(lx,1lx=1lm/m²),核心用于衡量物体表面接收光的密集程度。通过构建点光源照射的几何模型,可完成其严格推导:设点光源发光强度为I,在距离r处有微元面积dS,其法线与光线入射方向夹角为θ(入射角),则光源“看到”的有效面积为投影面积dScosθ。微元面积对光源所张立体角dΩ=dScosθ/r²,该立体角内的光通量dΦ=IdΩ,结合照度定义E=dΦ/dS,最终推导出照度公式E=Icosθ/r²。该公式同时包含两大核心定律:r²项体现的距离平方反比定律,表明照度随距离平方衰减;cosθ项体现的朗伯余弦定律,反映入射角对接收光密度的影响。
(四)亮度(L):光传播的相空间密度描述
亮度是光度学中最复杂且核心的物理量,其单位为cd/m²(1cd/m²=1lm/(sr·m²)),定义为发光表面在指定方向上,单位投影面积和单位立体角内传输的光通量。亮度不仅包含空间位置信息,还涵盖传播方向属性,是描述光在相空间(位置空间与方向空间)中联合分布密度的物理量。
通过“两步微分法”可推导其定义式:第一步通过方向微分锁定传播方向,定义发光强度I=dΦ/dΩ,确定光的角密度;第二步通过空间微分锁定发光面积,考虑视线与表面法线的夹角θ,取投影面积dAcosθ,将光强对投影面积微分得到亮度L=dI/(dAcosθ)。结合两步推导,最终得到亮度与光通量的二阶微分关系:L=d²Φ/(dΩ·dAcosθ),对应的光通量积分形式Φ=∫∫LdAcosθdΩ,该形式在渲染方程中应用广泛。需要注意的是,亮度与辐射度(Radiance)在数学定义和微分推导上完全同构,后者描述纯粹物理能量分布,而亮度是辐射度经人眼视见函数加权后的结果。
三、核心应用案例与定理验证
(一)朗伯体光出射度的证明
朗伯体(Lambertiansurface)是光学中常见的理想表面模型,其表面亮度L为常数。光出射度M定义为单位面积向半球空间辐射的总光通量,需通过积分推导其与亮度的关系:根据亮度定义dΦ=LdAcosθdΩ,光出射度M=Φ/dA=∫(半球空间)LcosθdΩ。代入微分立体角dΩ=sinθdθdφ,积分范围为φ∈[0,2π]、θ∈[0,π/2],因L为常数可提取积分外,计算得M=L·2π·∫(0到π/2)cosθsinθdθ。利用倍角公式化简积分项,最终得到M=πL,即朗伯体的光出射度为亮度的π倍,其关键原因是投影面积效应导致掠射角方向能量贡献衰减。
(二)亮度守恒定理的推导
在无介质吸收和散射的理想光学系统中,亮度具有守恒特性,该定理基于光管模型与光学扩展量守恒推导:考虑一束光在空间中传播,截面1面积为dA₁,立体角为dΩ₁;传播至截面2时,面积为dA₂,立体角为dΩ₂。由能量守恒,两截面光通量相等:Φ₁=Φ₂,结合亮度公式Φ=LdAcosθ(光线垂直截面时cosθ=1),得L₁dA₁dΩ₁=L₂dA₂dΩ₂。根据几何光学,光学扩展量Etendue=dAdΩ为守恒量,因此L₁=L₂,即亮度守恒。该定理的物理意义在于:被动光学系统无法使像的亮度超过光源表面亮度,确保了热力学第二定律在光学领域的适用性,例如透镜聚焦时,光斑面积减小必然伴随会聚角增大,亮度始终保持不变。
四、物理量关系网络与工程应用
(一)四大物理量的核心关联
四大物理量构成了层次分明的关系网络:光通量作为纯标量,描述光的总能量;发光强度是光通量对立体角的导数,仅包含方向信息,适用于点光源近似;照度是光通量对面积的导数,仅保留位置信息,用于表征表面受光密度;亮度作为相空间分布函数,融合了位置与方向信息,是信息最全面的物理量,也是连接其他物理量的核心枢纽。
(二)典型工程应用场景
1.亮度与发光强度的关联:亮度可理解为“发光强度的面密度”,当将显示器等面光源近似为点光源时,通过积分L=dI/(dAcosθ)可计算总光强,为面光源的光学性能评估提供依据。
2.照度与发光强度的关联:基于平方反比定律E=Icosθ/r²,可精准计算路灯、台灯等点光源在目标表面的照度,是照明系统设计的核心公式。
3.照度与亮度的关联:针对天空光等环境光,需通过积分E=∫(入射半球)LcosθdΩ计算照度,该关系是全局光照渲染(如路径追踪算法)的基础,广泛应用于计算机图形学领域。
光度学四大核心物理量的数学推导,建立在立体角微分形式的基础上,通过微积分工具构建了严谨的逻辑体系。从光通量的能量总量表征,到发光强度的方向密度描述,再到照度的表面受光量化,最终到亮度的相空间分布刻画,各物理量层层递进、相互关联,共同构成了光度学的理论框架。朗伯体光出射度证明与亮度守恒定理的应用,进一步验证了理论的科学性与实用性。深入理解这些物理量的定义、推导及关联,是开展复杂光学设计(如车灯、投影仪光路设计)与计算机图形学渲染的先决条件,对推动相关工程领域的技术创新具有重要意义。
-
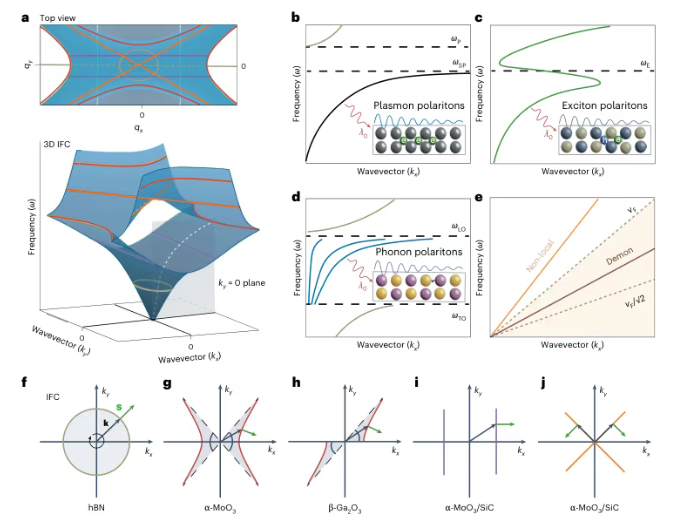
强各向异性范德华材料:纳米尺度下的光学新范式
在纳米光学领域的快速发展进程中,强各向异性范德华(vanderWaals,vdW)材料凭借其独特的物理特性,正重新定义折射、反射和聚焦等基本光学现象,为光子学应用开辟了全新赛道。发表于《Nature Nanotechnology》,系统深入地揭示了这类材料中极化激元的特殊行为及其引发的突破性光学效应,为纳米光子器件的创新发展奠定了重要基础。
2026-02-03
-

光学透镜加工出现颜色差异如何解?
光学透镜加工出现颜色差异,核心是加工过程中透镜表面的光学薄膜(增透膜/反射膜等)或基底材料表面发生了物理/化学变化,也可能是加工工艺参数偏差导致的膜层厚度、均匀性异常,需按“先定位差异成因→再针对性工艺调整→最后验证整改效果”的思路解决,以下是分场景的成因分析和具体解决方案,覆盖镀膜环节(最主要成因)、机械加工环节、清洁与后处理环节三大核心场景,兼顾量产和小批量加工的实操性:
2026-02-03
-

光度学核心物理量的数学推导与应用探析
光度学作为建立在几何光学与辐射度量学基础上的严密学科,其核心价值在于精准描述光的传播规律及与物质的相互作用。光通量、发光强度、照度和亮度这四大物理量,构成了光度学的理论基石,其内在逻辑关系与数学推导不仅是学术研究的关键内容,更是光学设计、计算机图形学等工程领域的技术前提。本文将从立体角的微分定义出发,系统梳理四大物理量的数学本质、推导过程,并探讨其核心应用与实践价值。
2026-02-03
-

光学镜片钻孔工艺技术解析与应用指南
镜片钻孔工艺是光学制造领域关键加工环节之一,其核心目的主要有两方面:一是在玻璃基板及其他光学元件表面实现精准钻孔;二是为分束镜、透镜、滤光片等光学零件半成品加工孔洞,以满足后续夹持、连接与调整的装配需求。本文将系统梳理光学制造中主流的钻孔工艺技术,从原理、特点、参数及应用等维度进行详细解析,为相关行业选型提供参考。
2026-02-02







