光学镜头畸变的系统性解析!光学镜头畸变的定义、成因及计算方法
在光学成像领域,畸变作为一种常见的光学现象,对成像质量的几何准确性具有显著影响。本文将从定义、成因及计算方法三个维度,对光学镜头畸变进行系统阐述,旨在为相关领域的研究与应用提供理论参考。

一、光学畸变(OpticalDistortion)的核心特征
1.定义界定
光学畸变是镜头光学系统固有的几何像差,其本质是物体通过镜头成像后,像的几何形状与原物体的理想图像产生非比例变形。需明确的是,这种畸变仅改变成像形状,不影响成像清晰度,与成像模糊现象存在本质区别。
2.成因分析
光学畸变的产生源于镜头像场中央区域与边缘区域的放大倍率不一致,这种不一致性由多种因素共同作用导致,包括镜头设计参数、光圈位置分布及光学系统的复杂程度等。
在理想镜头模型(如针孔模型)中,像高与物高呈线性比例关系,即像高h=f·tanθ(其中f为镜头焦距,θ为视场角),放大率保持恒定。但在实际镜头中,受镜片曲率、折射率分布及镜片组合方式的限制,离轴光线(大视场角)与轴上光线(小视场角)的放大率存在差异:
当离轴放大率小于轴上放大率时,实际像高h′<f·tanθ,产生桶形畸变,表现为图像边缘向内收缩,此现象在广角镜头中较为常见。
当离轴放大率大于轴上放大率时,实际像高h′>f·tanθ,产生枕形畸变,表现为图像边缘向外扩张,长焦镜头常出现此类畸变。
部分复杂镜头可能出现波浪形畸变,即局部区域同时存在桶形与枕形畸变特征。
3.计算方法
光学畸变的量化指标为畸变率,其计算公式如下:
畸变率=((h′−h)/h)×100%
式中,h表示按针孔模型计算的理想像高,h′表示镜头实际成像的像高。计算结果为负值时,对应桶形畸变;为正值时,对应枕形畸变。该指标直观反映了理想像与实际像的偏差程度,常被标注于镜头规格参数中,为镜头选型提供重要参考。
二、TV畸变(TelevisionDistortion)的特性解析
TV畸变主要用于描述图像自身的扭曲程度,其关注点为图形本身的变形情况,与光学畸变(侧重于实际图形与理想图形的差异)存在明显区分。
在实际应用中,TV畸变的计算存在不同标准:
SMIATV畸变(基于StandardMobileImagingArchitecture标准)的计算公式为:SMIATVDistortion=100(A−B)/B,其中A=(A1+A2)/2。
ISOTV畸变(传统TV畸变)的计算公式为:D_TV=(Δh/(2h))·100%。
在实际测量操作中,由于光学畸变的测量难度较大,对于实物镜头,通常以TV畸变作为主要测量指标,因其能更直接地反映图像自身的变形状况。
三、总结
光学畸变与TV畸变作为描述镜头成像几何特性的重要指标,在镜头设计、选型及图像后期处理中具有重要应用价值。深入理解二者的定义、成因及计算方法,有助于在摄影、机器视觉等领域优化成像效果,提升精密检测的准确性,为相关技术的发展提供理论支撑。
-

半导体抛光设备自动化应用及工艺质量管控要点探析
在半导体器件规模化量产进程中,抛光工艺作为保障晶圆加工精度与表面质量的核心环节,其设备自动化水平、工艺参数调控能力、检测体系完善度及异常处置效率,直接决定生产效率、工艺稳定性与产品良率。本文从抛光设备自动化配置要求、核心工艺参数调控、关键检测指标界定及常见工艺异常处理四个维度,系统阐述半导体抛光工艺的质量管控核心要点,为半导体抛光制程的标准化、精细化实施提供参考。
2026-02-12
-
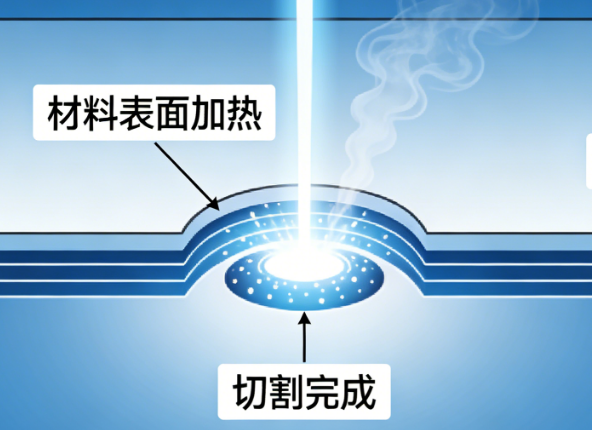
硅晶圆激光切割核心技术深度解析:原理、工艺与质量把控
在半导体制造产业链中,硅晶圆切割是芯片成型的关键工序,其加工精度与效率直接影响芯片良品率和产业发展节奏。随着微电子器件向微型化、薄型化升级,传统切割方式的弊端逐渐显现,激光切割凭借高精度、低损伤的技术优势成为行业主流。本文从激光切割系统的硬件构成出发,深入拆解隐形切割与消融切割两大核心工艺,解析光斑、焦点的精度控制逻辑,并探讨切割质量的评价维度与效率平衡策略,系统梳理硅晶圆激光切割的核心技术体系
2026-02-12
-
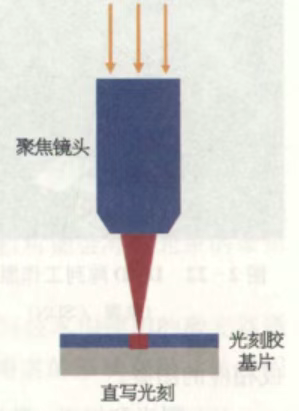
无掩模激光直写技术研究概述
无掩模激光直写技术作为微纳加工领域的先进光刻技术,摒弃了传统光刻工艺对掩模版的依赖,凭借直接写入的核心特性,在复杂微纳结构制备、高精度图案加工中展现出独特优势,成为微纳加工领域的重要技术方向。本文从工作原理与流程、技术特性、现存挑战、分辨率与对准参数、核心设备及厂务动力配套要求等方面,对该技术进行全面梳理与阐述。
2026-02-12
-

SiC功率器件的高温时代:封装成为行业发展核心瓶颈
在半导体功率器件技术迭代进程中,碳化硅(SiC)凭借高温工作、高电流密度、高频开关的核心优势,成为推动功率半导体升级的关键方向,其普及大幅提升了器件的功率密度与工作效率,为功率半导体行业发展带来全新机遇。但与此同时,行业发展的核心瓶颈正悄然从芯片设计与制造环节,转移至封装层面。当SiC将功率器件的工作温度与功率密度不断推高,芯片本身已具备承受更高应力的能力,而封装环节的材料适配、热路径设计等问题却日益凸显,高温与快速功率循环叠加的工况下,焊料与热路径成为决定SiC功率模块寿命的核心因素,封装技术的发展水平,正成为制约SiC功率器件产业化落地与长期可靠应用的关键。
2026-02-12







