光学成像的核心基石:点扩散函数(PSF)的发展、原理与价值
在光学成像技术的演进历程中,点扩散函数(PointSpreadFunction,PSF)是贯穿始终的核心概念。它的诞生标志着物理学从几何光学向波动光学的范式跨越,其物理机制与数学表征则为现代光学成像理论奠定了坚实基础,深刻定义了人类通过光学系统感知世界的边界与可能。从天文观测中的恒星成像到显微技术下的微观探索,PSF始终是连接物理实体与感知图像的关键桥梁,揭示了“完美成像”在物理规律下的本质局限与科学内涵。
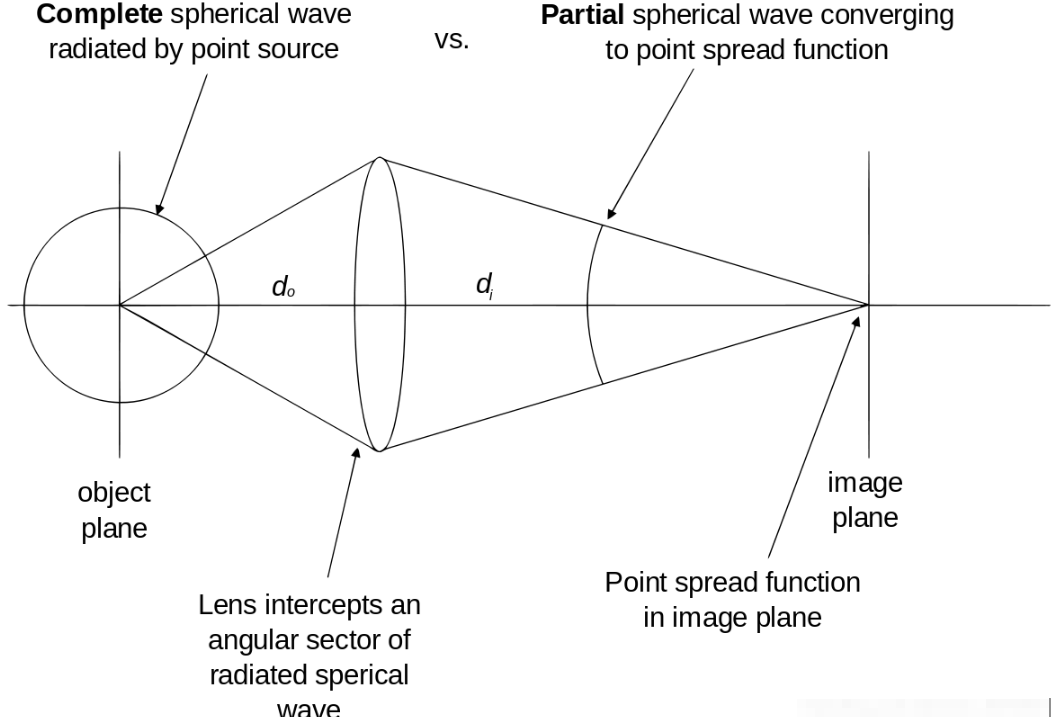
一、历史溯源:从现象探索到理论确立
PSF的形成与发展,是科学家们突破传统认知、揭示光的波动本质的过程,三大关键突破共同构建了其理论框架。
1835年,英国皇家天文学家乔治·比德尔·艾里(GeorgeBiddellAiry)的研究揭开了PSF的物理序幕。当时,天文学界普遍困惑于恒星观测中的“虚假盘”现象——理想点光源经望远镜成像后,并未呈现几何意义上的“点”,而是中心明亮、周围环绕暗环的光斑,且孔径越小光斑越大。艾里跳出“透镜工艺缺陷”的固有认知,基于光的波动理论与菲涅耳衍射理论,通过精密数学推导(后归纳为贝塞尔函数),首次证实该光斑是光波经圆形孔径衍射后的必然结果,即“艾里斑”。他提出的第一暗环角半径公式,不仅完美解释了“孔径与光斑大小”的反比关系,更揭示了核心真相:成像模糊并非工艺瑕疵,而是光的波动本性导致的物理必然。这一发现实质催生了PSF的概念,证明光学系统对“点”的成像本质是能量扩散的过程。
1873年,德国物理学家恩斯特·阿贝(ErnstAbbe)将这一现象升华为系统的成像理论。作为蔡司光学工厂的首席科学家,阿贝在显微成像研究中发现,即便消除了球差、色差等像差,极细微结构的成像仍存在不可突破的模糊极限。通过衍射光栅实验,他提出显微成像是“衍射-干涉”双重过程:光照射物体后衍射为不同空间频率分量,物镜收集这些分量并在像平面干涉,方可重构图像细节,且至少需收集0级与1级衍射光才能形成有效图像。基于此,阿贝定义了显微镜横向分辨率公式,建立了PSF宽度与数值孔径(NA)的反比关系,明确分辨率仅取决于光的波长与NA,与放大倍率无关,彻底打破了当时盲目追求高倍率的行业迷思。这一理论确立了波动光学在显微成像领域的主导地位,为现代显微光学奠定了理论基石。
1879年,英国物理学家瑞利勋爵(LordRayleigh)进一步完善了PSF的实用价值。他聚焦“两个相邻点光源何时可被分辨”这一工程核心问题,基于非相干成像下光强线性叠加的原理,提出了经典的瑞利判据:当一个点光源的艾里斑中心恰好落在另一个点光源的第一暗环上时,两光斑峰值间的光强凹陷约为26.5%,足以被人眼或探测器区分,此时定义为“刚能分辨”。这一判据并非绝对物理定律,而是兼顾观测实际的“实用阈值”,将艾里斑的数学性质转化为可操作的物理标准。其衍生的横向分辨率公式,与阿贝极限相互补充,前者关注“感知对比度”,后者聚焦“频率传递极限”,共同为光学系统性能评估提供了量化依据。
二、物理原理:PSF的多层级数学表征与衍射本质
现代光学视角下,成像系统本质是线性空间移不变系统(LSI),PSF作为系统的脉冲响应,其形态与特性由光的衍射规律、系统结构参数共同决定,可通过系统层、物理层、频域层三个维度深入解析。
在系统层,PSF的核心价值体现于基于线性叠加原理的卷积模型。该模型建立在两大关键假设之上:一是线性假设,非相干成像(如荧光显微镜、天文观测)中,图像总光强为各点光源独立成像光强的线性叠加,因光子间无显著相互作用;二是移不变性假设,在等晕区范围内,光学系统像差分布恒定,PSF形态不随点光源在物面的位置变化而改变。满足这两个条件时,成像过程可精确描述为物体强度分布与PSF的卷积运算(含噪声项)。这一模型彻底重构了“像”的本质:图像并非物体的完美复制,而是经PSF“低通滤波”后的结果,PSF的空间展宽直接决定了系统对高频细节(物体精细结构)的传递能力,从信息论角度定义了成像分辨率的极限。
在物理层,PSF的形态是光波经光学系统光瞳后的衍射产物,其数学表达依赖衍射理论。对于低数值孔径(LowNA)且满足近轴近似的常规系统,标量衍射理论可提供足够精确的描述:像平面复振幅分布是广义瞳孔函数(含孔径形状、透过率及波像差)的二维傅里叶变换,而PSF(光强分布)则是该复振幅模的平方。理想圆形孔径对应的PSF即为艾里斑,其径向强度分布由第一类一阶贝塞尔函数描述,第一暗环位置与光波长、孔径尺寸直接相关。当系统数值孔径较高(NA>0.7)时,近轴近似失效,光波的矢量特性不可忽略,需采用Richards-Wolf矢量衍射积分描述:大角度会聚光线会产生正交偏振分量与纵向电场分量,导致PSF旋转对称性破坏,主瓣展宽,分辨率理论极限略有下降。
在频域层,传递函数(OTF/MTF)是PSF的重要补充表征。根据卷积定理,空域中的卷积运算对应频域中的乘法运算。光学传递函数(OpticalTransferFunction,OTF)作为PSF的傅里叶变换,全面描述系统对不同空间频率成分的传递能力。OTF可分解为模与辐角两部分:调制传递函数(ModulationTransferFunction,MTF)作为OTF的模,描述不同空间频率正弦光栅成像后的对比度衰减,低频时MTF测量归一化为1,随频率升高逐渐下降,直至截止频率(分辨率极限);相位传递函数(PhaseTransferFunction,PTF)作为OTF的相位部分,描述空间频率成分的成像位置偏移,理想系统的PTF多为零或线性项,非线性PTF则会导致图像畸变或不对称模糊。空域PSF与频域OTF的对应关系,构建了光学系统性能评估的完整体系。
三、核心价值与现实意义
PSF不仅是光学成像的基础理论概念,更在工程实践与科学探索中具有不可替代的价值。从本质而言,任何光学系统都是基于PSF的低通滤波器,其性能上限由光的波长与系统孔径共同定义——这一规律划定了人类通过光学手段探索微观世界(如细胞结构、原子尺度)与宏观宇宙(如遥远星系、恒星演化)的物理边界,让我们深刻认识到“完美成像”在自然规律下的不可能性。
在技术应用中,PSF的理论为光学系统设计提供了核心指导:通过优化瞳孔函数(如改变光阑形状、引入相位板),可“定制”PSF形态以适配特定成像需求;基于MTF的性能评估,能精准量化光学系统的分辨率与对比度传递能力,为望远镜、显微镜、相机等设备的研发提供量化依据。同时,PSF也是超分辨成像技术的核心理论基础,现代超分辨技术本质上都是通过突破传统PSF的衍射极限,实现更高精度的细节探测。
值得注意的是,现实中的光学系统往往受球差、慧差、像散等像差影响,这些像差会扭曲、拉伸甚至破坏理想的艾里斑形态,导致PSF特性偏离理论模型。因此,深入研究像差对PSF的影响,是光学工程领域的重要课题,对提升实际成像系统的性能具有关键意义。
点扩散函数(PSF)的发展历程,是物理学理论突破与工程实践探索相互促进的典范。从艾里斑的发现到阿贝衍射理论的建立,再到现代傅里叶光学与矢量衍射理论的完善,PSF的内涵不断丰富,始终引领着光学成像技术的进步。未来,随着像差校正技术、超分辨成像技术、计算光学的持续发展,人们对PSF的调控能力将不断提升,有望在更广阔的领域突破传统成像极限。
后续研究将聚焦两大方向:一是系统分析球差、慧差等实际像差对PSF形态的影响机制,建立更精准的误差修正模型;二是通过数值仿真与实验验证,探索PSF的定制化设计与优化方法,为新型光学成像系统的研发提供理论支撑。PSF作为光学成像的核心基石,将持续在科学探索与技术创新中发挥关键作用,推动人类对世界的认知不断迈向更深层次。
-

半导体抛光设备自动化应用及工艺质量管控要点探析
在半导体器件规模化量产进程中,抛光工艺作为保障晶圆加工精度与表面质量的核心环节,其设备自动化水平、工艺参数调控能力、检测体系完善度及异常处置效率,直接决定生产效率、工艺稳定性与产品良率。本文从抛光设备自动化配置要求、核心工艺参数调控、关键检测指标界定及常见工艺异常处理四个维度,系统阐述半导体抛光工艺的质量管控核心要点,为半导体抛光制程的标准化、精细化实施提供参考。
2026-02-12
-
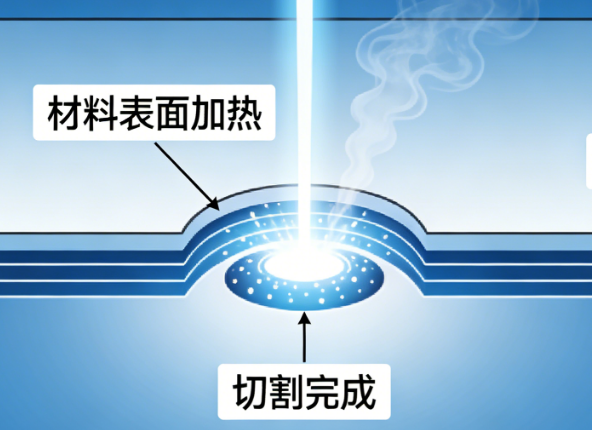
硅晶圆激光切割核心技术深度解析:原理、工艺与质量把控
在半导体制造产业链中,硅晶圆切割是芯片成型的关键工序,其加工精度与效率直接影响芯片良品率和产业发展节奏。随着微电子器件向微型化、薄型化升级,传统切割方式的弊端逐渐显现,激光切割凭借高精度、低损伤的技术优势成为行业主流。本文从激光切割系统的硬件构成出发,深入拆解隐形切割与消融切割两大核心工艺,解析光斑、焦点的精度控制逻辑,并探讨切割质量的评价维度与效率平衡策略,系统梳理硅晶圆激光切割的核心技术体系
2026-02-12
-
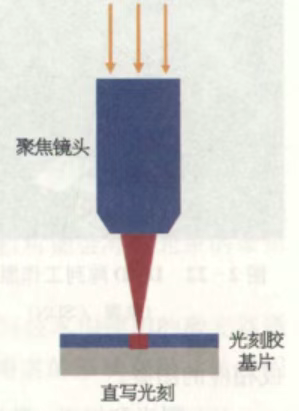
无掩模激光直写技术研究概述
无掩模激光直写技术作为微纳加工领域的先进光刻技术,摒弃了传统光刻工艺对掩模版的依赖,凭借直接写入的核心特性,在复杂微纳结构制备、高精度图案加工中展现出独特优势,成为微纳加工领域的重要技术方向。本文从工作原理与流程、技术特性、现存挑战、分辨率与对准参数、核心设备及厂务动力配套要求等方面,对该技术进行全面梳理与阐述。
2026-02-12
-

SiC功率器件的高温时代:封装成为行业发展核心瓶颈
在半导体功率器件技术迭代进程中,碳化硅(SiC)凭借高温工作、高电流密度、高频开关的核心优势,成为推动功率半导体升级的关键方向,其普及大幅提升了器件的功率密度与工作效率,为功率半导体行业发展带来全新机遇。但与此同时,行业发展的核心瓶颈正悄然从芯片设计与制造环节,转移至封装层面。当SiC将功率器件的工作温度与功率密度不断推高,芯片本身已具备承受更高应力的能力,而封装环节的材料适配、热路径设计等问题却日益凸显,高温与快速功率循环叠加的工况下,焊料与热路径成为决定SiC功率模块寿命的核心因素,封装技术的发展水平,正成为制约SiC功率器件产业化落地与长期可靠应用的关键。
2026-02-12







