光学系统设计中对称性与反对称性的核心机制:像差校正逻辑与量产可行性分析
在光学工程领域,从消费电子的手机成像模组、专业光学的显微物镜,到工业检测的高精度镜头,光学系统的成像性能、制造成本及生产良率,均取决于设计阶段对“对称性”与“反对称性”的核心决策。部分系统可容忍微米级加工误差,量产良率稳定在90%以上;而部分系统对误差极度敏感,良率常低于50%。本文基于像差理论的数学本质,系统剖析对称设计、反对称设计的内在原理与工程特性,并构建一套可直接应用于实践的系统潜力评估框架,为光学设计与量产落地提供理论支撑与实操指南。

一、理论基础:像差的奇偶性分类与设计逻辑关联
光学系统的成像缺陷(即像差),本质是实际波前与理想球面波前的偏差,可用波像差函数(W(H,rho,theta))定量描述(其中(H)为归一化视场坐标,(rho)为出瞳归一化半径,(theta)为出瞳极角)。通过对波像差函数进行幂级数展开,可依据数学特性将像差划分为“奇像差”与“偶像差”两类,这一分类是后续设计选择的底层理论依据。
1.奇像差:非轴对称的形态畸变源
奇像差的波像差多项式中,包含(H)(视场)或(rho)(出瞳半径)的奇次幂项,典型代表为彗差、畸变。其核心特征是破坏像点的轴对称性:彗差会使轴外点成像呈现“彗星状”弥散斑,导致像点形态失真;畸变则使平面物体成像产生“梯形”“桶形”或“枕形”变形,直接影响成像的几何准确性。此类像差的非轴对称特性,决定了其校正逻辑与系统的几何对称性密切相关。
2.偶像差:轴对称的能量弥散源
偶像差的波像差多项式中,包含(H)或(rho)的偶次幂项,主要包括球差、场曲、像散(部分高阶像散项除外)。其核心特征是保持像差的轴对称分布:球差导致不同孔径高度的光线聚焦于光轴上不同位置,使像点沿光轴方向弥散;场曲使平面物体的理想像面呈现为曲面,导致视场边缘与中心无法同时清晰成像;像散则使轴外点在两个正交子午面内的聚焦位置不同,形成椭圆形弥散斑。此类像差的轴对称特性,需通过光焦度的合理分配实现校正。
二、对称设计:基于几何镜像的固有稳健性系统
对称设计的定义为“光学系统关于孔径光阑平面呈近似镜像对称”,典型结构包括双高斯镜头、对称式望远物镜等。其核心优势在于对奇像差的被动抵消能力,以及由此带来的公差不敏感性,是兼顾性能与量产性的经典设计范式。
1.工作机制:镜像结构的奇像差抵消原理
孔径光阑作为对称设计的“对称轴”,将系统分为前、后两个镜像对称的子系统。当光线经过前子系统时,产生的奇像差(如彗差系数(+COM)、畸变系数(+DIS)),会在后子系统中被大小相等、符号相反的奇像差((COM)、(DIS))精准抵消。这一过程无需额外引入校正元件,完全依赖几何对称性实现,本质是“前子系统的像差贡献与后子系统的像差贡献形成矢量相反”,最终使系统总奇像差趋近于零。
2.数学本质:公差敏感度的二阶效应特性
在光学制造与装配中,偏心(δ)、倾斜(ε)、厚度偏差(▲d))等公差,可视为对“理想对称状态”的微小扰动。设系统像差系数(S)为公差参数的函数(S(delta,varepsilon,Deltad)),在理想对称点((δ=0,ε=0,▲d=0)),像差系数对各公差参数的一阶偏导数均为零,即:

这表明,对称系统的像差变化与公差量的平方成正比(二阶效应)。即使存在微小加工误差(如(δ=0.1text{mm})),其对像差的影响仅为(0.01mm^2)量级,而非线性关系下的(0.1mm)量级。这种“误差影响的平方衰减特性”,使对称系统具备天然的公差容错性,微小误差仅导致性能缓慢衰退,而非急剧恶化,为高量产良率提供了理论保障。
3.工程局限性:偶像差的累积效应与单独校正需求
对称设计的镜像结构虽能抵消奇像差,但会对偶像差产生“累积叠加效应”:前子系统产生的球差、场曲等偶像差,会与后子系统产生的同符号偶像差叠加,导致系统总偶像差增大。因此,对称系统的偶像差无法通过对称性抵消,必须在每个子系统内部单独校正——例如双高斯镜头需通过优化前、后子系统中透镜的曲率半径、材料折射率及厚度,分别抑制球差与场曲,否则会因偶像差累积导致成像清晰度下降。
三、反对称设计:基于光焦度配对的高性能校正系统
当系统受限于结构约束(如显微物镜的光阑外置、反远距镜头的长后工作距需求),无法实现几何对称时,反对称设计成为高性能成像的核心解决方案。其定义为“通过正负光焦度元件的合理配对,实现像差主动校正的设计范式”,核心逻辑是利用正负光焦度对偶像差的反向贡献,构建像差平衡机制。
1.工作机制:正负光焦度的偶像差反向抵消
正透镜与负透镜对偶像差的贡献具有天然反向性:正透镜(光焦度(+))会产生负球差((SA))与向光轴凹陷的场曲((FC));负透镜(光焦度(phi))则产生正球差((+SA))与向光轴凸起的场曲((+FC))。通过将正负透镜按特定顺序组合(如“负正”“正负正”),可使二者的偶像差贡献相互抵消,实现球差、场曲的主动校正。例如反远距镜头采用“负透镜前置、正透镜后置”的结构,既通过负透镜扩展视场、满足长后工作距需求,又通过正负光焦度的球差反向抵消,保证边缘视场的成像清晰度。
2.关键前提:灵敏度匹配的工程实现
反对称设计的性能优势并非天然存在,其核心前提是“灵敏度匹配”——若前子系统灵敏度(如孤立强负透镜与弱正透镜组合),则总像差变化,后子系统无法对前子系统的误差形成有效补偿,系统仍保持高公差敏感度。因此,光学设计师需通过多变量优化(如调整透镜曲率、厚度、材料折射率),使前、后子系统的像差灵敏度系数绝对值近似相等,才能激活反对称设计的误差平衡效应。
四、非对称设计:极限性能导向的工程挑战
非对称设计指“无几何对称结构、无光焦度反对称配对”的自由设计范式,通常用于满足特殊性能需求(如非常规视场、异形孔径的工业检测镜头)。但其设计与量产面临两大核心挑战,限制了其大规模应用。
1.公差敏感度的一阶效应
非对称系统的像差系数对公差参数的一阶偏导数不为零。这意味着微小加工误差会直接导致像差产生同量级的变化,系统性能随误差线性衰退,公差容错性远低于对称与反对称设计。
2.优化过程的局部极小值困境
非对称系统的设计变量(透镜数量、曲率、厚度、间距、材料等)通常多于对称与反对称系统,形成高维参数空间。优化算法在迭代过程中,极易陷入“局部极小值”——即当前像差指标已无法通过参数微调进一步降低,但该状态并非全局最优解。处于局部极小值的系统,对加工误差极为敏感:微小参数偏差会使系统脱离局部极小值,导致像差急剧增大,最终表现为量产良率低下(通常低于50%)。
五、实践评估框架:光学系统潜力的多维度判断方法
基于上述理论,可通过观察系统的外形结构、光焦度分布及透镜形态,快速评估其性能潜力与量产可行性,为设计方案筛选与风险预判提供实操工具。
1.整体架构评估:几何对称性的稳健性判断
判断依据:观察系统是否关于孔径光阑呈现镜像对称或近似对称。
潜力评估:若满足对称条件(如双高斯结构),则系统在奇像差控制与公差容错性上具备先天优势,加工装配误差对性能的影响较小,量产良率通常可达到80%以上,属于“高稳健性设计”;若不满足对称条件,则需进一步评估光焦度分布,判断是否为反对称设计。
2.光焦度分布评估:反对称性的性能潜力判断
判断依据:分析光阑前后的光焦度序列,是否存在“正负”“负正”或“正负正”等有序交替分布。
潜力评估:若光焦度呈反对称分布,则系统具备主动校正偶像差的能力,性能潜力较高(如反远距镜头的“负正”组合);若光焦度分布无规律(如“正正负”“负负正”),则可能存在像差校正不充分的问题,需警惕边缘视场画质衰退风险。
3.透镜形态评估:关键元件的校正能力判断
强弯月透镜:若光阑附近存在凸面相对的强弯月透镜,表明系统在主动控制像散与场曲(佩兹瓦尔和),此类透镜的复杂面型可有效抑制高阶像差,是“高级像差校正”的典型特征。
胶合透镜组:胶合组(多片透镜通过光学胶粘合)本质是微型反对称单元,既能通过不同材料的色散差异校正色差,又能通过一体化结构降低装配公差,是“兼顾性能与量产性”的重要标志。
4.风险预警:高公差敏感度的特征识别
孤立强透镜:若系统中存在单一承担70%以上总光焦度的孤立强正/负透镜,表明该透镜的像差贡献占比极高,易产生残余像差(尤其是球差),且公差敏感度显著高于其他结构,量产良率风险较高。
极端曲率表面:若透镜表面曲率极大(接近半球面)或极小(接近平面),会导致加工难度骤增(如半球面的面型精度难以控制),且对镀膜均匀性、装配同轴度的要求极端苛刻,易引发成品报废。
光学系统设计中,对称与反对称并非对立选择,而是基于性能需求与量产约束的“平衡范式”:对称设计以几何镜像为核心,提供天然的公差稳健性,适合消费电子等大规模量产场景;反对称设计以光焦度配对为核心,通过主动校正实现高性能,适合显微物镜、专业相机等高精度场景;非对称设计则仅在特殊性能需求下作为补充,需通过精密制造缓解量产困境。
未来,随着人工智能光学设计(如基于深度学习的像差预测与参数优化)与超精密制造技术(如亚微米级光刻与离子束抛光)的融合,将实现“对称稳健性”与“反对称高性能”的高效结合——例如通过AI算法快速优化反对称系统的灵敏度匹配参数,通过超精密加工降低误差量级,最终突破“高性能与高量产性不可兼得”的传统限制。深入理解对称与反对称的本质机制,是推动光学系统向“更高性能、更低成本、更高良率”发展的关键基础。
-

半导体抛光设备自动化应用及工艺质量管控要点探析
在半导体器件规模化量产进程中,抛光工艺作为保障晶圆加工精度与表面质量的核心环节,其设备自动化水平、工艺参数调控能力、检测体系完善度及异常处置效率,直接决定生产效率、工艺稳定性与产品良率。本文从抛光设备自动化配置要求、核心工艺参数调控、关键检测指标界定及常见工艺异常处理四个维度,系统阐述半导体抛光工艺的质量管控核心要点,为半导体抛光制程的标准化、精细化实施提供参考。
2026-02-12
-
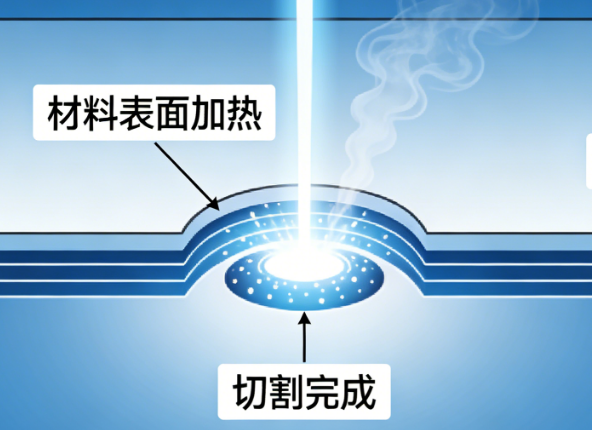
硅晶圆激光切割核心技术深度解析:原理、工艺与质量把控
在半导体制造产业链中,硅晶圆切割是芯片成型的关键工序,其加工精度与效率直接影响芯片良品率和产业发展节奏。随着微电子器件向微型化、薄型化升级,传统切割方式的弊端逐渐显现,激光切割凭借高精度、低损伤的技术优势成为行业主流。本文从激光切割系统的硬件构成出发,深入拆解隐形切割与消融切割两大核心工艺,解析光斑、焦点的精度控制逻辑,并探讨切割质量的评价维度与效率平衡策略,系统梳理硅晶圆激光切割的核心技术体系
2026-02-12
-
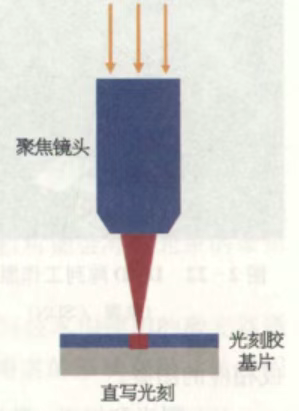
无掩模激光直写技术研究概述
无掩模激光直写技术作为微纳加工领域的先进光刻技术,摒弃了传统光刻工艺对掩模版的依赖,凭借直接写入的核心特性,在复杂微纳结构制备、高精度图案加工中展现出独特优势,成为微纳加工领域的重要技术方向。本文从工作原理与流程、技术特性、现存挑战、分辨率与对准参数、核心设备及厂务动力配套要求等方面,对该技术进行全面梳理与阐述。
2026-02-12
-

SiC功率器件的高温时代:封装成为行业发展核心瓶颈
在半导体功率器件技术迭代进程中,碳化硅(SiC)凭借高温工作、高电流密度、高频开关的核心优势,成为推动功率半导体升级的关键方向,其普及大幅提升了器件的功率密度与工作效率,为功率半导体行业发展带来全新机遇。但与此同时,行业发展的核心瓶颈正悄然从芯片设计与制造环节,转移至封装层面。当SiC将功率器件的工作温度与功率密度不断推高,芯片本身已具备承受更高应力的能力,而封装环节的材料适配、热路径设计等问题却日益凸显,高温与快速功率循环叠加的工况下,焊料与热路径成为决定SiC功率模块寿命的核心因素,封装技术的发展水平,正成为制约SiC功率器件产业化落地与长期可靠应用的关键。
2026-02-12







