线性畸变与光学畸变的本质差异及精密光学系统设计优化策略
在半导体光刻、工业计量镜头等精密光学系统的设计与验证过程中,普遍存在一项关键认知矛盾:软件优化报告显示光学畸变已得到有效控制时,实际投影图像却可能出现网格扭曲;而当投影网格实现完美横平竖直时,软件却会反馈显著的畸变数值。这一矛盾的核心症结,在于“线性投影工程要求”与“传统光学畸变评价体系”在定义内涵、基准设定及目标导向层面的根本差异。本文将系统剖析其内在原理,厘清核心概念边界,为精密光学系统的设计、验证提供规范化解决方案。
一、核心概念界定与计算框架辨析
要破解上述矛盾,需先明确四个相互关联且本质迥异的核心概念,并区分其所属的理论计算与物理现实两大框架。
(一)四大核心概念定义
1.理想模型(IdealModel):作为传统光学设计理论中的“完美成像”几何基准,其数学表达式为`y'_ideal=EFL×tan(θ)`,其中EFL为系统等效焦距,θ为视场角。该模型描述了无像差、光阑位于透镜上的理想薄透镜成像规律。
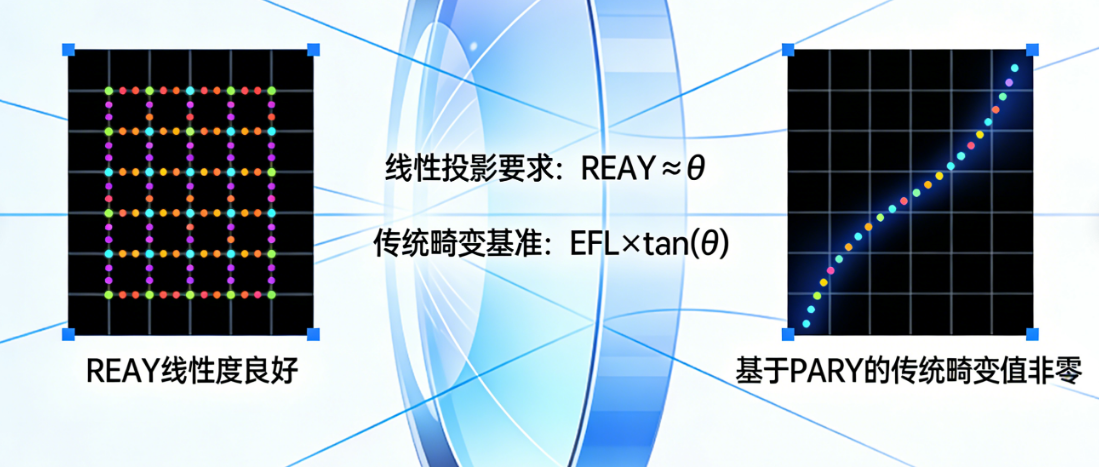
2.线性投影的数学本质:对于需严格保障几何保真度的投影系统,核心要求是成像前后物与像保持几何相似,即横向放大率β为常数。对于无穷远物,需消除理想模型中tan(θ)函数的非线性,强制实际主光线像高REAY与视场角θ成正比(`REAY=k×θ`,k为常数,扫描镜头中k即为焦距f,构成f-θ镜头)。若二者非线相关,物方等角度间隔的点在像面将呈现非等间距排列,直接导致图像变形。
3.近轴像高(PARY):并非通过`EFL×tan(θ)`直接计算,而是光学设计软件基于实际镜头结构(曲率、厚度、材料、光阑位置等),遵循近轴光学线性传递与折射公式(`n₁·θ₁≈n₂·θ₂`)进行近轴光线追迹后,在像面得到的交点坐标。其核心目标是逼近理想模型的`EFL×tan(θ)`值,为复杂实际光学结构求解等效理想薄透镜的像高参考。
4.实际像高(REAY):通过精确光线追迹计算得出的主光线实际落点坐标,严格遵循斯涅尔定律(`n₁·sin(θ₁)=n₂·sin(θ₂)`),完整涵盖初级与高级像差的影响,是决定成像几何形状、评价投影线性度与网格方正度的唯一物理依据。
(二)理论与物理层面的计算框架差异
| 计算层面 | 数学基础 | 计算过程 | 输出结果 |
|---|---|---|---|
| 理论层面 | 近轴近似(n₁·θ₁=n₂·θ₂) |
线性传递矩阵运算:光线状态(位置、角度)= 矩阵 × 前一状态 | PARY(近轴像高) |
| 物理层面 | 精确斯涅尔定律(n₁·sin(θ₁)=n₂·sin(θ₂)) |
非线性迭代求解:在每一光学表面解三角方程 | REAY(实际像高) |
需明确的是,传统光学畸变(Distortion)的计算公式为`Distortion=(REAY-PARY)/PARY×100%`,该指标衡量的是物理现实(REAY)与理论近似(PARY)之间的偏差,本质是基于近轴理论基准的相对误差评价。
二、矛盾根源解析与深层机制探究
(一)核心矛盾的本质:评价基准与工程目标的背离
线性投影的工程目标是实现`REAY`与θ的线性关系(`REAY∝θ`),而传统光学畸变评价的隐含基准是理想模型的非线性关系(`EFL×tan(θ)`)。这种基准层面的固有差异,导致完美满足线性投影要求的系统,其REAY必然系统性偏离`EFL×tan(θ)`曲线。将该线性REAY代入传统畸变公式,自然会得到非零且呈特定变化趋势的畸变值(如近似线性增长),这一结果反映的是两种成像模型的固有差异,而非设计缺陷。
(二)PARY波动的三重驱动因素
即便在未强制线性投影的传统设计中,优化后的畸变曲线也常出现细微波动,其核心原因是PARY作为计算基准并非稳定不变的理想值,而是受多重因素影响产生波动,具体机制如下:
1.理论层面:近轴近似的固有误差:近轴追迹依赖`sinθ≈θ`或`tanθ≈θ`的小角度近似,在有限大视场下,会引入与视场角高次方相关的确定性高阶误差。即便对无像差的完美镜头,其PARY结果与精确的`EFL×tan(θ)`仍存在理论偏差。
2.物理层面:高级像差的耦合干扰(核心驱动):光学系统不可避免存在高级像差,这些像差信息会融入优化后的镜头结构参数(曲率、间距等)。软件进行近轴追迹时,输入的表面数据已承载全部高级像差信息,其会微妙改变光线入射条件,通过近轴公式传递放大,导致PARY产生非线性微小波动。优化可精准控制REAY路径,但难以完全消除这种“算法污染”。
3.技术层面:数值计算的极限噪声:优化作为迭代过程,镜头参数在收敛点附近的极微小抖动(末位有效数字级),会导致PARY在微米或亚微米量级产生随机跳动,属于纯粹的数值计算噪声。
上述因素共同作用,使得即便REAY线性度已优化至微米级,畸变曲线仍可能呈现“弯弯曲曲”的形态,表明畸变曲线平坦度是与高级像差紧密相关的独立优化目标,与REAY几何线性度未必完全一致。
三、精密光学系统的设计策略与验证规范
针对追求严格几何保真度的光学设计,需建立以物理成像性能为核心的设计与验证体系,具体遵循以下原则:
(一)明确优化优先级与核心目标
1.核心目标:将REAY线性度作为首要优化方向,在优化函数中为多个视场点添加REAY操作数,明确设定目标值为`k×θ`或`β×y_object`,并赋予较高优化权重,这是实现精准投影的核心保障。
2.辅助目标:将传统畸变(DIMX)控制作为次要或辅助目标,可添加DIMX操作数并设目标值为0或特定常数,但权重需低于REAY操作数,避免优化器为追求畸变指标而破坏REAY线性度。
(二)建立本质性验证方法体系
1.直观验证(定性):利用网格畸变分析功能,忽略软件自动绘制的参考网格与偏差彩色向量,仅观察实际光线交点(彩色点)构成的图案。若这些点排列为均匀完美方格,则表明系统实际线性投影性能达标。
2.精准验证(定量):导出各视场的REAY值,计算线性度误差`[REAY/(k×θ)-1]×100%`,该指标需直接满足系统规格要求(如小于0.01%),是衡量成像几何精度最本质、最可靠的性能指标。
(三)确立合理的设计预期与指标体系
1.接受正常波动:理解软件报告的畸变值(PARY/DIMX)受理论模型与计算局限性影响,当REAY线性度已达极佳水平时,其曲线出现±0.05%以内的微小波动属于正常现象,无需过度追求绝对平坦。
2.区分指标属性:交付或评审时,需同时提供“REAY线性度误差”与“传统光学畸变值”两项指标,并明确界定:前者是决定实际成像几何精度的核心性能指标,后者是参照传统理论的参考性报告指标。
线性畸变(几何保真度)与光学畸变(理论符合度)的本质差异,是光学设计理论模型与工程实践需求之间张力的集中体现。软件报告的光学畸变值,是基于内部近轴计算基准的理论参考指标;而投影图像的几何真实性,仅由实际光线行为(REAY)唯一决定。
对于半导体光刻、工业计量等精密投影与测量系统,必须以REAY线性度为优化核心,以网格畸变图的实际成像效果与线性度误差为验收准绳,才能确保设计方案切实满足最终应用场景的性能要求,为精密光学系统的设计与验证提供可靠的技术路径。
-
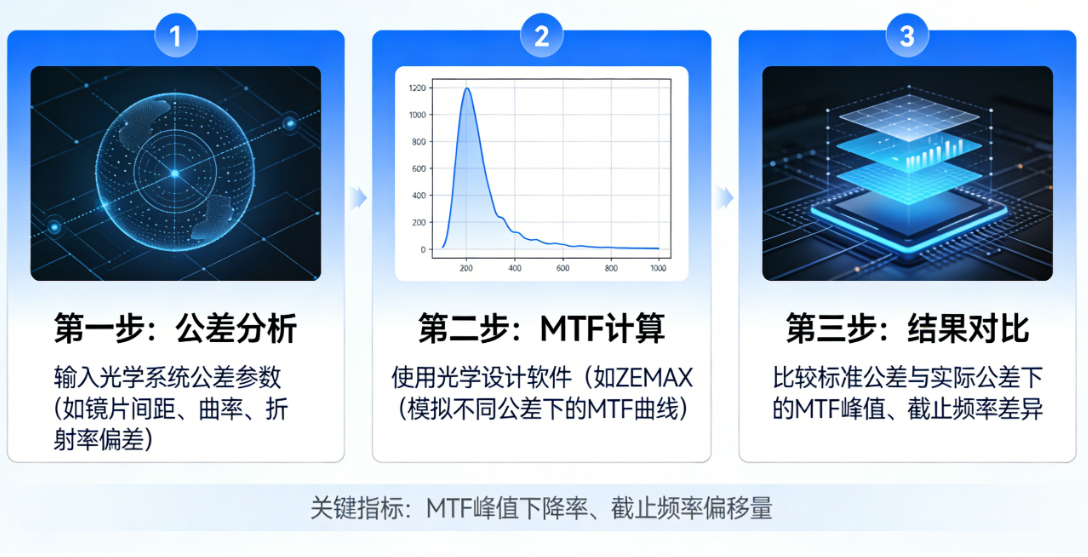
如何评估光学系统公差对MTF的影响?
评估光学系统公差对调制传递函数(MTF)的影响是光学设计中从“理论完美”走向“工程量产”的关键环节。这一过程通常被称为公差灵敏度分析(ToleranceSensitivityAnalysis)和蒙特卡洛分析(MonteCarloAnalysis)。
2026-02-27
-
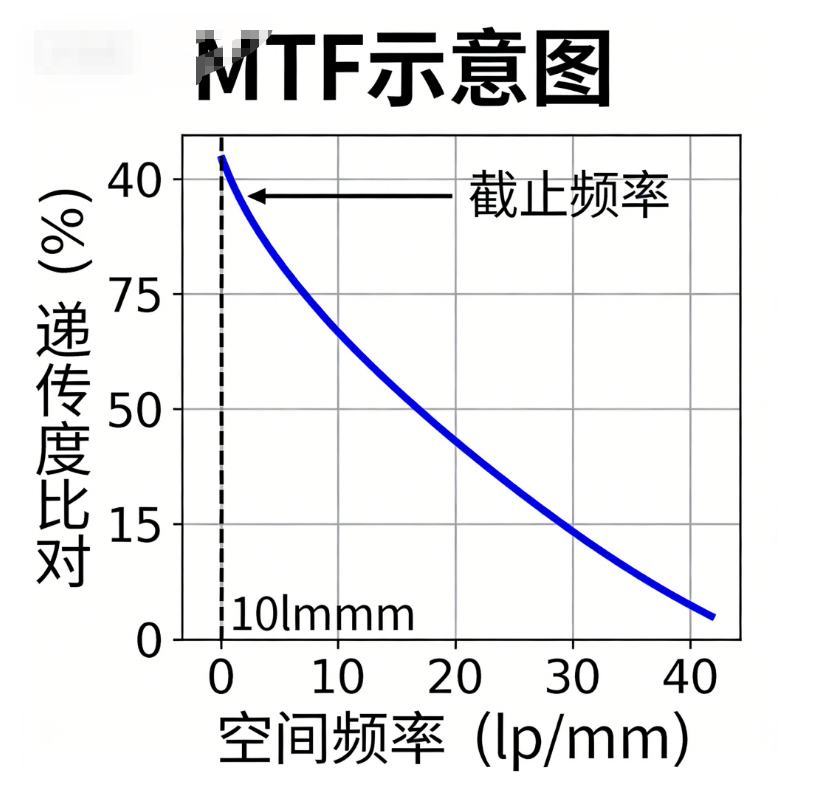
调制传递函数(MTF)在光学系统设计中的核心作用与应用分析
调制传递函数(ModulationTransferFunction,MTF)已成为评价光学系统成像质量最权威、最客观的量化指标。本文旨在深入探讨MTF的理论基础,系统阐述其在光学设计流程中的关键作用,包括像质评价、系统优化、公差分析及光电匹配等方面,并论证其作为连接理论设计与实际成像效果桥梁的核心地位。
2026-02-27
-

彭德里与超材料、变换光学科普,打破物理边界的电磁学革命
在现代电磁学与光学的发展历程中,约翰·彭德里(JohnPendry)的名字成为了一个标志性符号。他所开创的超材料与变换光学理论框架,突破了自然界材料对电磁响应的固有物理限制,将人类对光与物质相互作用的认知,从被动寻找天然材料推向了主动设计几何结构以自由调控光场的全新阶段,不仅重构了宏观电磁学的设计范式,更为诸多前沿学科与工业应用开辟了全新道路
2026-02-26
-

从凸透镜到复杂镜头组,一文读懂有效焦距的精密测量
在光学制造与检测领域,有效焦距(EffectiveFocalLength,EFL)是表征透镜及光学系统成像性能的核心参数。针对正值焦距(会聚系统)与负值焦距(发散系统)的测量难题,传统几何光学方法往往存在操作繁琐、精度受限及无法统一测量平台等弊端。本文基于德国TRIOPTICS公司研发、由欧光科技(福建)有限公司提供的OptiSpheric®通用途光学测量仪(全自动数字测焦仪),深入探讨其在正负焦距高精度测量中的技术原理、性能指标及工业应用价值,旨在为光学检测提供标准化的技术参考。
2026-02-26







