折射率怎么会是复数呢?
我们生活在现实世界中,所接触的数字大多是纯实数。然而,在科学研究的领域里,数学家们发现了复数的独特优势——利用复数能够极大地简化分析单频系统的数学运算,这种分析方法通常被称为时谐分析或频域分析。在频域中研究电磁场或光学时,许多物理量会以复数形式呈现,这样便能同时表示相位和振幅,而复折射率正是其中一个典型例子。

在+z方向上传播的波,在频域中可写成E(z)=E0exp(-kk0nz)),其中k0=25π/λ0是真空波数,λ0为真空波长。复折射率n以n=no-jk的形式表示,这里的实部no被称为寻常折射率,虚部k则叫做消光系数。将其代入波的频域方程,便能深入探究E的特性。
进一步考察方程右边,可明晰实部与虚部的物理意义。寻常折射率no的行为与我们在将\n视为复数之前对折射率的认知极为相似,它决定了波的速度,或者说决定了波作为位置函数的振荡速度。而消光系数k则掌控着波随距离衰减的速度——当介质存在吸收损耗时,波会逐渐衰减,此时消光系数量化了这种损耗;值得注意的是,负的消光系数描述的是增益情况,即当介质提供能量时,波的强度不仅不会衰减,反而会增强。
复折射率通过实部与虚部的巧妙分工,分别刻画了波的传播特性与能量变化(衰减或增益),成为频域分析中处理电磁学或光学问题的关键工具,展现了复数在科学分析中简化问题、深化理解的强大能力。
-

半导体抛光设备自动化应用及工艺质量管控要点探析
在半导体器件规模化量产进程中,抛光工艺作为保障晶圆加工精度与表面质量的核心环节,其设备自动化水平、工艺参数调控能力、检测体系完善度及异常处置效率,直接决定生产效率、工艺稳定性与产品良率。本文从抛光设备自动化配置要求、核心工艺参数调控、关键检测指标界定及常见工艺异常处理四个维度,系统阐述半导体抛光工艺的质量管控核心要点,为半导体抛光制程的标准化、精细化实施提供参考。
2026-02-12
-
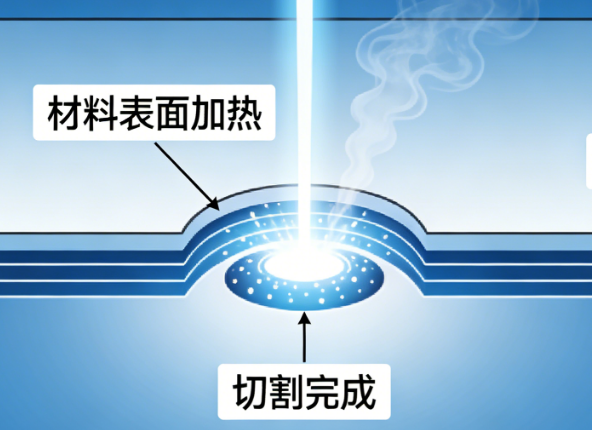
硅晶圆激光切割核心技术深度解析:原理、工艺与质量把控
在半导体制造产业链中,硅晶圆切割是芯片成型的关键工序,其加工精度与效率直接影响芯片良品率和产业发展节奏。随着微电子器件向微型化、薄型化升级,传统切割方式的弊端逐渐显现,激光切割凭借高精度、低损伤的技术优势成为行业主流。本文从激光切割系统的硬件构成出发,深入拆解隐形切割与消融切割两大核心工艺,解析光斑、焦点的精度控制逻辑,并探讨切割质量的评价维度与效率平衡策略,系统梳理硅晶圆激光切割的核心技术体系
2026-02-12
-
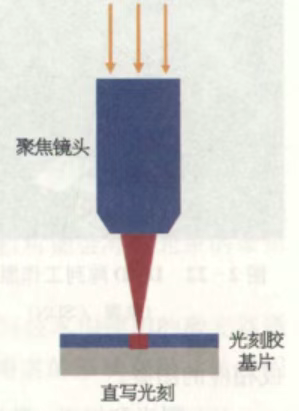
无掩模激光直写技术研究概述
无掩模激光直写技术作为微纳加工领域的先进光刻技术,摒弃了传统光刻工艺对掩模版的依赖,凭借直接写入的核心特性,在复杂微纳结构制备、高精度图案加工中展现出独特优势,成为微纳加工领域的重要技术方向。本文从工作原理与流程、技术特性、现存挑战、分辨率与对准参数、核心设备及厂务动力配套要求等方面,对该技术进行全面梳理与阐述。
2026-02-12
-

SiC功率器件的高温时代:封装成为行业发展核心瓶颈
在半导体功率器件技术迭代进程中,碳化硅(SiC)凭借高温工作、高电流密度、高频开关的核心优势,成为推动功率半导体升级的关键方向,其普及大幅提升了器件的功率密度与工作效率,为功率半导体行业发展带来全新机遇。但与此同时,行业发展的核心瓶颈正悄然从芯片设计与制造环节,转移至封装层面。当SiC将功率器件的工作温度与功率密度不断推高,芯片本身已具备承受更高应力的能力,而封装环节的材料适配、热路径设计等问题却日益凸显,高温与快速功率循环叠加的工况下,焊料与热路径成为决定SiC功率模块寿命的核心因素,封装技术的发展水平,正成为制约SiC功率器件产业化落地与长期可靠应用的关键。
2026-02-12







